Note: Written by the late great John Eargle (and re-published courtesy of Harman Professional), this article is excerpted from Chapter 1 of a book he co-authored with Chris Foreman entitled Audio Engineering for Sound Reinforcement. Eargle was JBL’s vice-president of engineering for many years and was a well-known author and consultant. He was also a skilled recording engineer with more than 250 CD releases and his cinema work garnered him a Technical Oscar in 2001. Eargle’s books are industry benchmarks.
Let’s begin with the most basic question: What is sound? For our purposes, we will define sound as fluctuations, or variations, in air pressure over the audible range of human hearing. This is normally taken as the frequency range from about 20 cycles per second up to about 20,0a00 cycles per second. The term Hertz (abbreviated Hz) is universally used to indicate cycles per second. Likewise, the term kiloHertz (kHz) indicates 1,000 Hz. We can write 20,000 Hz simply as 20 kHz.
A two-to-one frequency ratio is called an octave, a term taken from music notation. For example, the frequency band from 1 kHz to 2 kHz comprises one octave. A frequency decade represents a 10-to-one frequency ratio.
The speed of sound propagation in air at normal temperature is approximately 1,130 feet per second (344 meters per second). At higher temperatures, the speed of sound increases slightly, while at lower temperatures, the speed is less. The precise values for the speed of sound in air are given by the following equations:
Speed at 0° Fahrenheit = 1,052 feet/second (+ 1.106 feet per degree above 0° F)
Speed at 0° Centigrade = 331.3 meters/second (+ 0.607m per degree above °0 C)
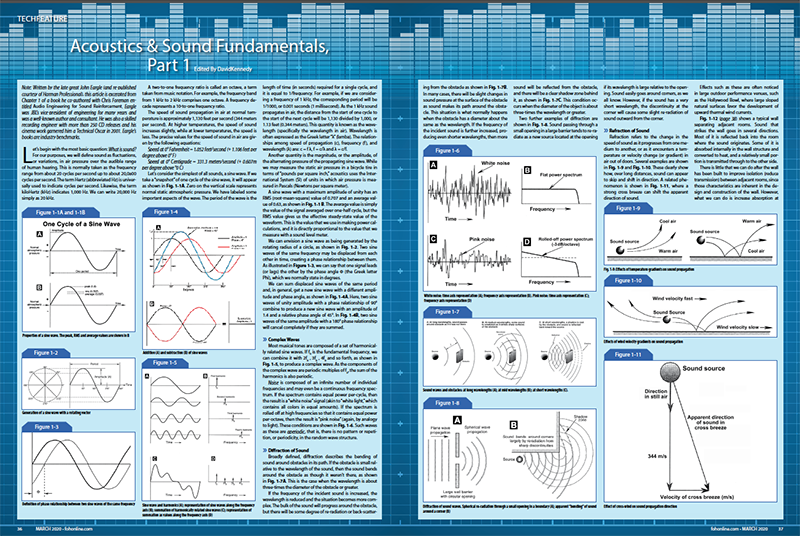
Let’s consider the simplest of all sounds, a sine wave. If we take a “snapshot” of one cycle of the sine wave, it will appear as shown in Fig. 1-1A. Zero on the vertical scale represents normal static atmospheric pressure. We have labeled some important aspects of the wave. The period of the wave is the length of time (in seconds) required for a single cycle, and it is equal to 1/frequency. For example, if we are considering a frequency of 1 kHz, the corresponding period will be 1/1000, or 0.001 seconds (1 millisecond). As the 1 kHz sound propagates in air, the distance from the start of one cycle to the start of the next cycle will be 1,130 divided by 1,000, or 1.13 feet (0.344 meters). This quantity is known as the wavelength (specifically the wavelength in air). Wavelength is often expressed as the Greek letter “λ” (lamba). The relationships among speed of propagation (c), frequency (f), and wavelength (λ) are: c = f λ, f = c/λ and λ = c/f.
Another quantity is the magnitude, or the amplitude, of the alternating pressure of the propagating sine wave. While we may measure the static air pressure in a bicycle tire in terms of “pounds per square inch,” acoustics uses the International System (SI) of units in which air pressure is measured in Pascals (Newtons per square meter).
A sine wave with a maximum amplitude of unity has an RMS (root-mean-square) value of 0.707 and an average value of 0.63, as shown in Fig. 1-1 B. The average value is simply the value of the signal averaged over one-half cycle, but the RMS value gives us the effective steady-state value of the waveform. This is the value that we use in making power calculations, and it is directly proportional to the value that we measure with a sound level meter.
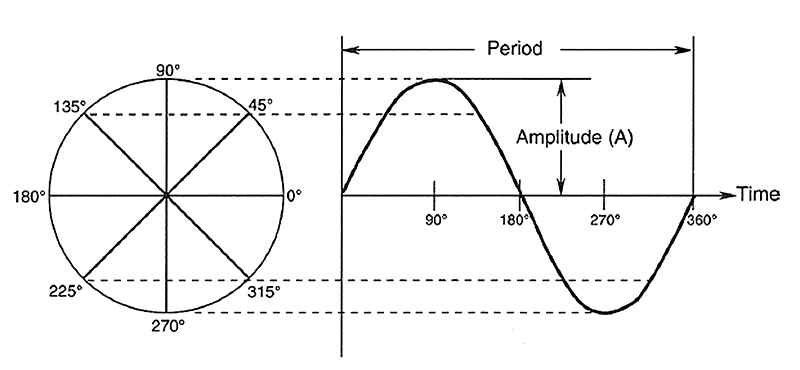
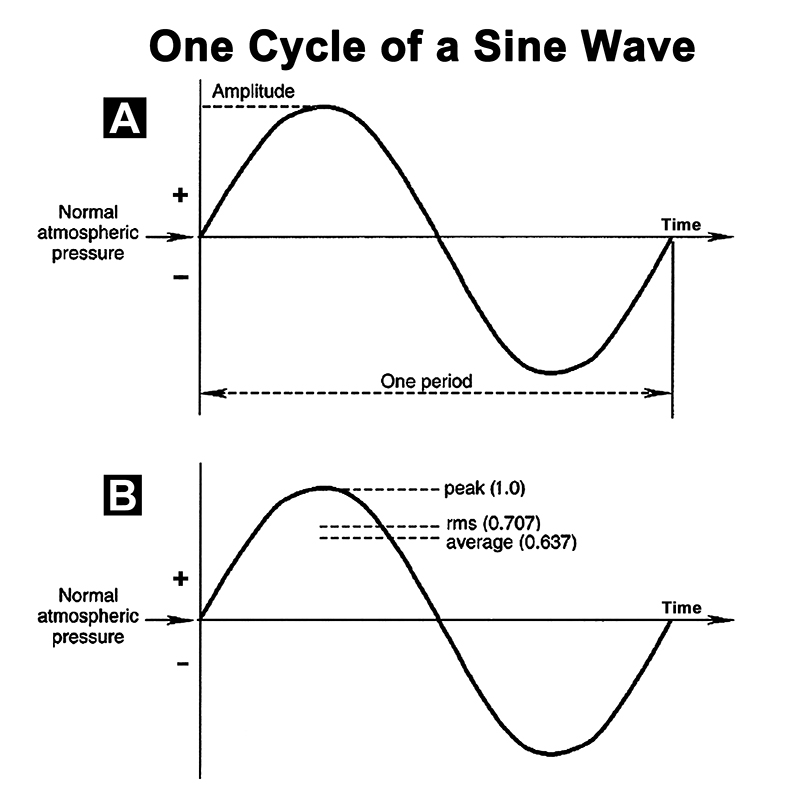
We can envision a sine wave as being generated by the rotating radius of a circle, as shown in Fig. 1-2. Two sine waves of the same frequency may be displaced from each other in time, creating a phase relationship between them.
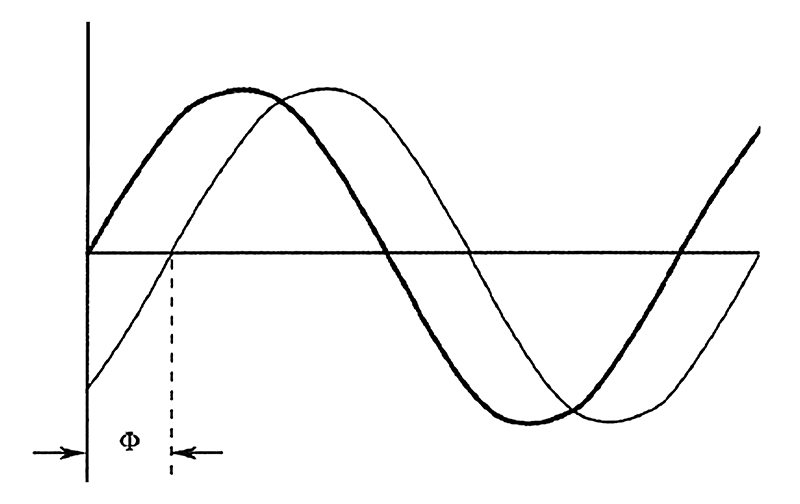
As illustrated in Figure 1-3, we can say that one signal leads (or lags) the other by the phase angle Ф (the Greek letter Phi), which we normally state in degrees.
We can sum displaced sine waves of the same period and, in general, get a new sine wave with a different amplitude and phase angle, as shown in Fig. 1-4A. Here, two sine waves of unity amplitude with a phase relationship of 90° combine to produce a new sine wave with an amplitude of 1.4 and a relative phase angle of 45°.
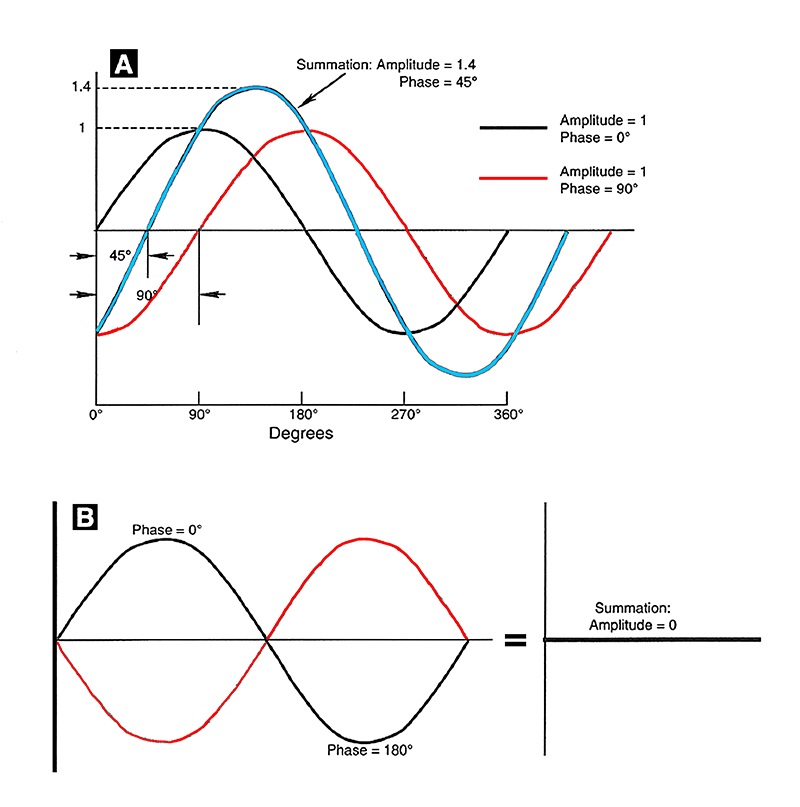
In Fig. 1-4B, two sine waves of the same amplitude with a 180° phase relationship will cancel completely if they are summed.
Complex Waves
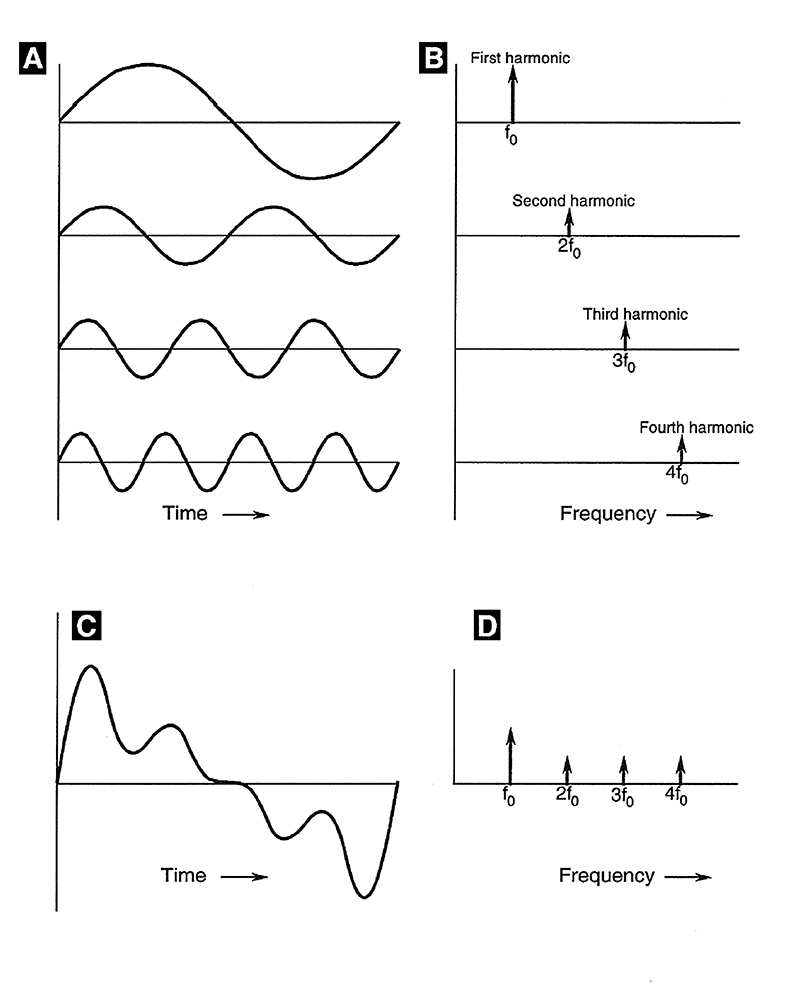
Most musical tones are composed of a set of harmonically related sine waves. If fo is the fundamental frequency, we can combine it with 2fo , 3fo , 4fo and so forth, as shown in Fig. 1-5, to produce a complex wave. As the components of the complex wave are periodic multiples of fo, the sum of the harmonics is also periodic.
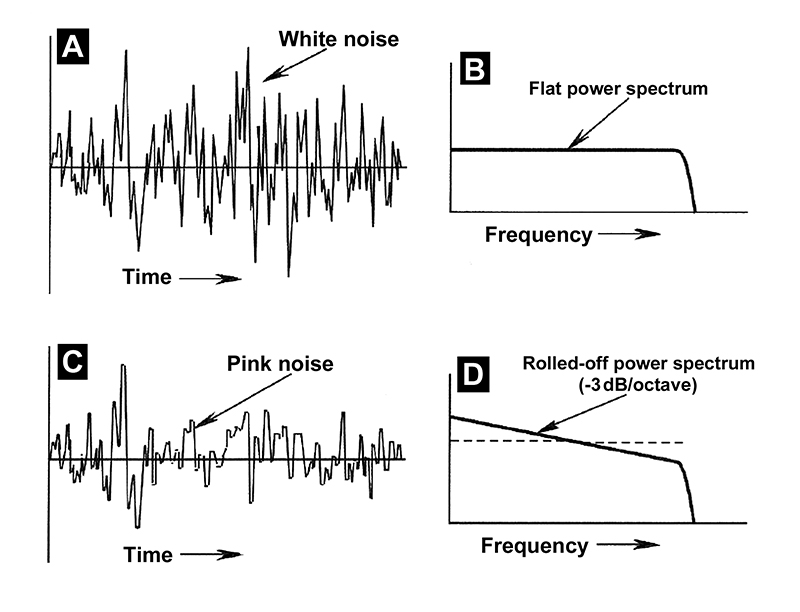
Noise is composed of an infinite number of individual frequencies and may even be a continuous frequency spectrum. If the spectrum contains equal power per-cycle, then the result is a “white noise” signal (akin to “white light,” which contains all colors in equal amounts). If the spectrum is rolled off at high frequencies so that it contains equal power per-octave, then the result is “pink noise” (again, by analogy to light). These conditions are shown in Fig. 1-6. Such waves as these are aperiodic, that is, there is no pattern or repetition, or periodicity, in the random wave structure.

Diffraction of Sound
Broadly defined, diffraction describes the bending of sound around obstacles in its path. If the obstacle is small relative to the wavelength of the sound, then the sound bends around the obstacle as though it weren’t there, as shown in Fig. 1-7A. This is the case when the wavelength is about three-times the diameter of the obstacle or greater.
If the frequency of the incident sound is increased, the wavelength is reduced and the situation becomes more complex. The bulk of the sound will progress around the obstacle, but there will be some degree of re-radiation or back-scattering from the obstacle as shown in Fig. 1-7B. In many cases, there will be slight changes in sound pressure at the surface of the obstacle as sound makes its path around the obstacle. This situation is what normally happens when the obstacle has a diameter about the same as the wavelength. If the frequency of the incident sound is further increased, producing even shorter wavelengths, then more sound will be reflected from the obstacle, and there will be a clear shadow zone behind it, as shown in Fig. 1-7C. This condition occurs when the diameter of the object is about three-times the wavelength or greater.

Two further examples of diffraction are shown in Fig. 1-8. Sound passing through a small opening in a large barrier tends to re-radiate as a new source located at the opening if its wavelength is large relative to the opening. Sound easily goes around corners, as we all know. However, if the sound has a very short wavelength, the discontinuity at the corner will cause some slight re-radiation of sound outward from the corner.
Refraction of Sound
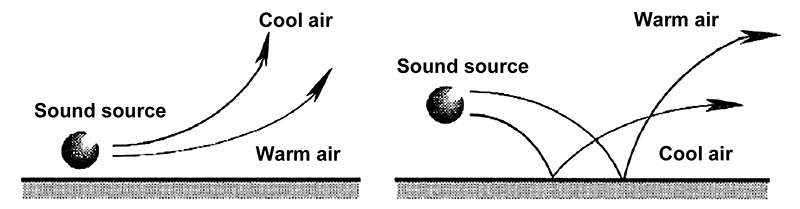
Refraction refers to the change in the speed of sound as it progresses from one medium to another, or as it encounters a temperature or velocity change (or gradient) in air out of doors. Several examples are shown in Fig. 1-9 and Fig. 1-10. These clearly show how, over long distances, sound can appear to skip and shift in direction.
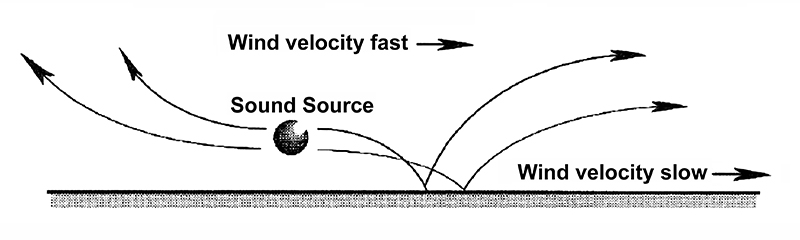
A related phenomenon is shown in Fig. 1-11, where a strong cross breeze can shift the apparent direction of sound.
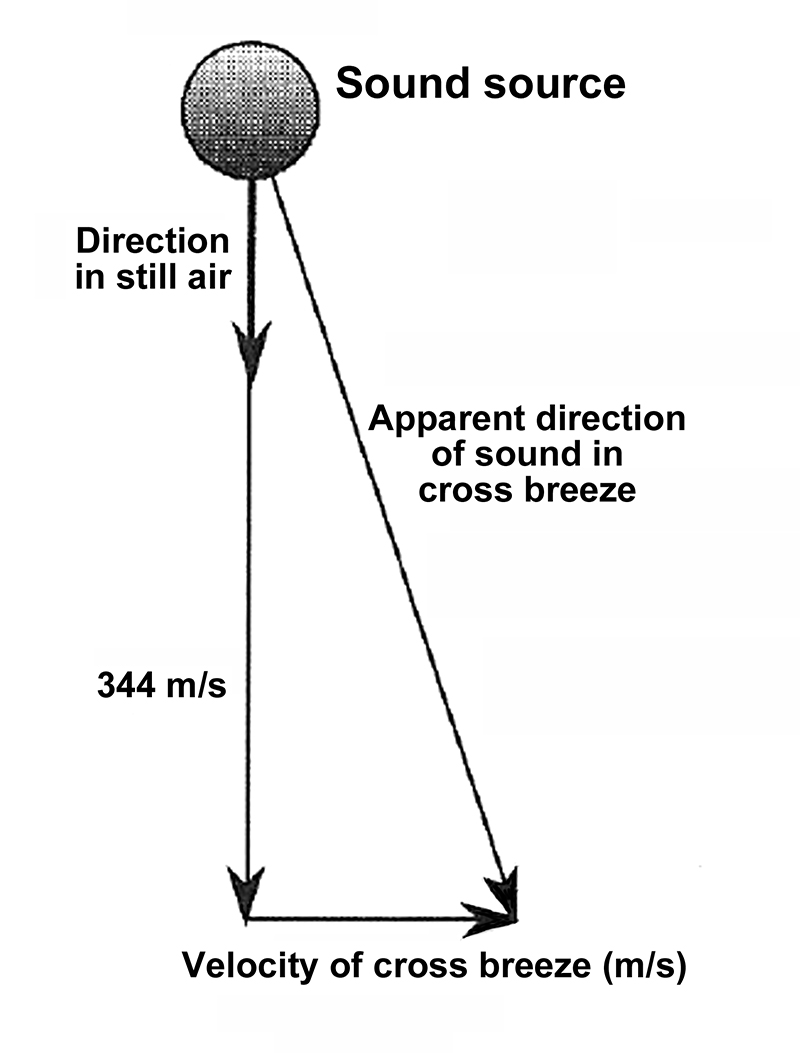
Effects such as these are often noticed in large outdoor performance venues, such as the Hollywood Bowl, where large sloped natural surfaces favor the development of upward thermal wind currents.

Fig. 1-12 (page 38) shows a typical wall separating adjacent rooms. Sound that strikes the wall goes in several directions. Most of it is reflected back into the room where the sound originates. Some of it is absorbed internally in the wall structure and converted to heat, and a relatively small portion is transmitted through to the other side.
There is little that we can do after the wall has been built to improve isolation (reduce transmission) between adjacent rooms, since those characteristics are inherent in the design and construction of the wall. However, what we can do is increase absorption at the surface and reduce reflections coming back into the originating room. This can take the form of externally applied damping materials, such as Fiberglas battens or multiple folds of heavy drapery.
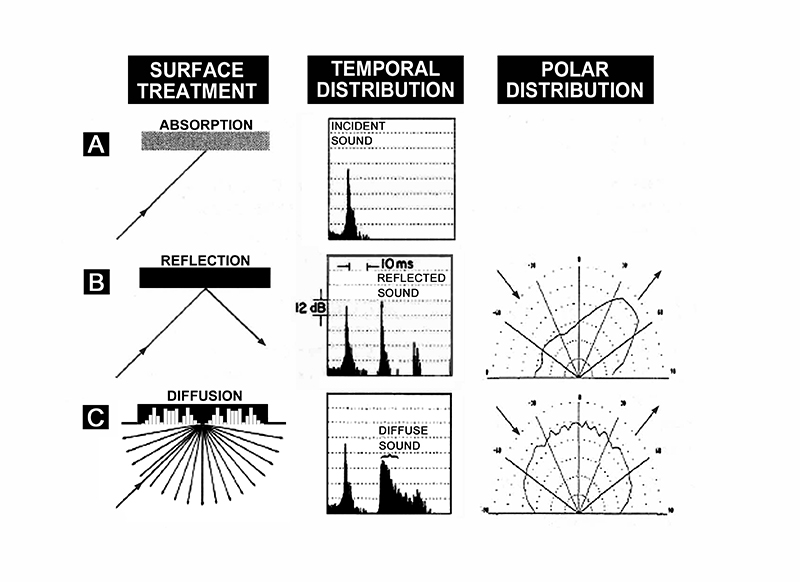
The reflection of sound from a wall normally involves some degree of scattering. In Fig. 1-13A, we see what happens when sound of a fairly short wavelength strikes an absorptive surface at an oblique angle. Most of the sound is absorbed, but some rebounds at an angle equal to the angle of incidence. In Fig. 1-13B we see what happens when the wall surface has very little absorption; most of the rebounding sound is concentrated at the complementary angle, but some is re-radiated at adjacent angles.
We also know that sound striking irregular surfaces tends to scatter to a large degree. When the surface has been mathematically designed to maximize this effect, as in Fig. 1-13C, the sound is essentially reradiated in all directions in the plane of reflection. The specific diffusing surface illustrated here is the quadratic residue diffuser (Schroeder, 1984; D’Antonio, 1984).
Absorption Coefficient, Defined
Acousticians use the term “absorption coefficient” to describe the ratio of acoustical power absorbed to the total sound striking a boundary. For example, a surface with an absorption coefficient of 0.3 will reflect 0.7 of the power and absorb the remaining fraction of 0.3. If the surface has an absorption coefficient of 0.1, it will absorb 10 percent of the power and reflect the remaining 90 percent. The sound power that is absorbed at the boundary merely becomes heat; normally, some of the power is transmitted through the boundary and is re-radiated as sound on the other side of that boundary.
Absorption coefficients normally range between zero (no absorption) and 1 (total absorption), and published values for many materials and surface finishes are given in acoustical handbooks over several octave bandwidths covering the range from 125 Hz to 8 kHz. The Greek symbol alpha, “α”, is used to indicate an absorption coefficient. (The concept will be expanded in Part 2 of this article, next month.)

To download a PDF of this tech feature, CLICK HERE.
To reach tech editor David Kennedy go to www.immersive-pa.com.



